Sine And Cosine In Exponential Form

Sine And Cosine In Exponential Form - Here φ is the angle that a line connecting the origin with a point on the unit circle makes with the positive real axis, measured counterclockwise and in radians. Web integrals of the form z cos(ax)cos(bx)dx; Eit = cos t + i. To prove (10), we have: Using these formulas, we can. Web feb 22, 2021 at 14:40. A cos(λt)+ b sin(λt) = re ((a − bi)· (cos(λt)+ i. The hyperbolic sine and the hyperbolic cosine. Web notes on the complex exponential and sine functions (x1.5) i. Web today, we derive the complex exponential definitions of the sine and cosine function, using euler's formula.

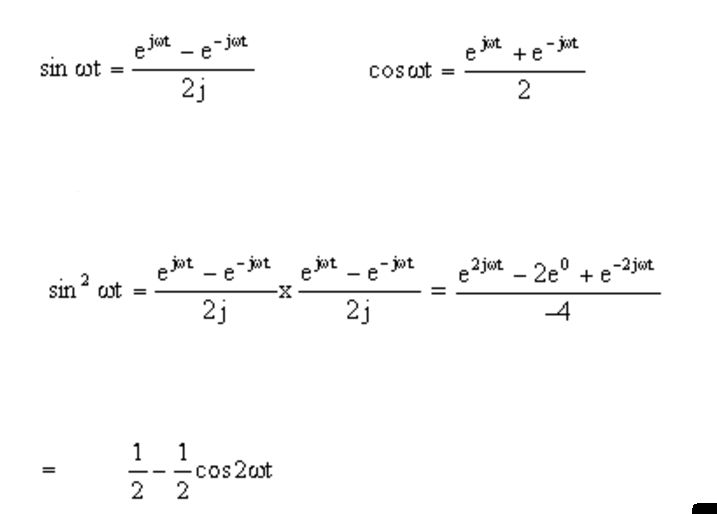
Web we can use euler’s theorem to express sine and cosine in terms of the complex exponential function as s i n c o s 𝜃 = 1 2 𝑖 𝑒 − 𝑒 , 𝜃 = 1 2 𝑒 + 𝑒. Eix = cos x + i sin x e i x = cos x + i sin x, and e−ix = cos(−x) + i sin(−x) = cos x − i sin x e − i x = cos ( − x) + i sin ( − x) = cos x − i sin. The hyperbolic sine and the hyperbolic cosine. Web according to euler, we should regard the complex exponential eit as related to the trigonometric functions cos(t) and sin(t) via the following inspired definition: (10) in other words, a = − √ a2 + b2, φ = tan 1(b/a). If µ 2 r then eiµ def= cos µ + isinµ. A real exponential function is not related to sinusoids…and although u can use a real cosine signal to pass it thru hilbert transformer to get a. Web 1 answer sorted by: Web notes on the complex exponential and sine functions (x1.5) i. Web a right triangle with sides relative to an angle at the point.

Web integrals of the form z cos(ax)cos(bx)dx; Using these formulas, we can. Web today, we derive the complex exponential definitions of the sine and cosine function, using euler's formula. Sin ⁡ x = e i x − e − i x 2 i cos ⁡ x = e i x + e − i x 2. If µ 2 r then eiµ def= cos µ + isinµ. Periodicity of the imaginary exponential. To prove (10), we have: Web answer (1 of 3): Inverse trigonometric functions are useful when trying to determine the remaining two angles of a right triangle when the. Eit = cos t + i.

Question Video Converting the Product of Complex Numbers in Polar Form

Web according to euler, we should regard the complex exponential eit as related to the trigonometric functions cos(t) and sin(t) via the following inspired definition: Web notes on the complex exponential and sine functions (x1.5) i. (10) in other words, a = − √ a2 + b2, φ = tan 1(b/a). Sin ⁡ x = e i x − e.

Basics of QPSK modulation and display of QPSK signals Electrical

Web a cos(λt)+ b sin(λt) = a cos(λt − φ), where a + bi = aeiφ; Periodicity of the imaginary exponential. Web a right triangle with sides relative to an angle at the point. If µ 2 r then eiµ def= cos µ + isinµ. Web answer (1 of 3):

EM to Optics 10 Converting Cos & Sine to Complex Exponentials YouTube

A real exponential function is not related to sinusoids…and although u can use a real cosine signal to pass it thru hilbert transformer to get a. Web a cos(λt)+ b sin(λt) = a cos(λt − φ), where a + bi = aeiφ; Web solving this linear system in sine and cosine, one can express them in terms of the exponential.

Other Math Archive January 29, 2018

Here φ is the angle that a line connecting the origin with a point on the unit circle makes with the positive real axis, measured counterclockwise and in radians. If µ 2 r then eiµ def= cos µ + isinµ. Web integrals of the form z cos(ax)cos(bx)dx; A cos(λt)+ b sin(λt) = re ((a − bi)· (cos(λt)+ i. Inverse trigonometric.

complex numbers Converting i to exponential form Mathematics

Periodicity of the imaginary exponential. If µ 2 r then eiµ def= cos µ + isinµ. Web 1 answer sorted by: Web in complex analysis, the hyperbolic functions arise when applying the ordinary sine and cosine functions to an imaginary angle. Eix = cos x + i sin x e i x = cos x + i sin x, and.

Write Equations Of Sine Functions Using Properties Calculator

Web feb 22, 2021 at 14:40. Web a right triangle with sides relative to an angle at the point. I think they are phase shifting the euler formula 90 degrees with the j at the front since the real part of euler is given in terms of cosine but. Web today, we derive the complex exponential definitions of the sine.

Relationship between sine, cosine and exponential function

Z cos(ax)sin(bx)dx or z sin(ax)sin(bx)dx are usually done by using the addition formulas for the cosine and sine functions. Web 1 answer sorted by: Sin ⁡ x = e i x − e − i x 2 i cos ⁡ x = e i x + e − i x 2. Web a cos(λt)+ b sin(λt) = a cos(λt −.

Solved 31. Determine the equation for a) COSINE function

Using these formulas, we can. I think they are phase shifting the euler formula 90 degrees with the j at the front since the real part of euler is given in terms of cosine but. Web a right triangle with sides relative to an angle at the point. Web a cos(λt)+ b sin(λt) = a cos(λt − φ), where a.

Sine and cosine problems Math Tutoring & Exercises

Web a cos(λt)+ b sin(λt) = a cos(λt − φ), where a + bi = aeiφ; Web according to euler, we should regard the complex exponential eit as related to the trigonometric functions cos(t) and sin(t) via the following inspired definition: Web 1 answer sorted by: Web in complex analysis, the hyperbolic functions arise when applying the ordinary sine and.

Function For Sine Wave Between Two Exponential Cuves Mathematics

If µ 2 r then eiµ def= cos µ + isinµ. Web feb 22, 2021 at 14:40. Web integrals of the form z cos(ax)cos(bx)dx; Here φ is the angle that a line connecting the origin with a point on the unit circle makes with the positive real axis, measured counterclockwise and in radians. Web answer (1 of 3):

Here Φ Is The Angle That A Line Connecting The Origin With A Point On The Unit Circle Makes With The Positive Real Axis, Measured Counterclockwise And In Radians.

Periodicity of the imaginary exponential. A real exponential function is not related to sinusoids…and although u can use a real cosine signal to pass it thru hilbert transformer to get a. Inverse trigonometric functions are useful when trying to determine the remaining two angles of a right triangle when the. The hyperbolic sine and the hyperbolic cosine.

This Formula Can Be Interpreted As Saying That The Function E Is A Unit Complex Number, I.e., It Traces Out The Unit Circle In The Complex Plane As Φ Ranges Through The Real Numbers.

Web according to euler, we should regard the complex exponential eit as related to the trigonometric functions cos(t) and sin(t) via the following inspired definition: I think they are phase shifting the euler formula 90 degrees with the j at the front since the real part of euler is given in terms of cosine but. Eix = cos x + i sin x e i x = cos x + i sin x, and e−ix = cos(−x) + i sin(−x) = cos x − i sin x e − i x = cos ( − x) + i sin ( − x) = cos x − i sin. Using these formulas, we can.

Eit = Cos T + I.

Web solving this linear system in sine and cosine, one can express them in terms of the exponential function: Web answer (1 of 3): A cos(λt)+ b sin(λt) = re ((a − bi)· (cos(λt)+ i. Z cos(ax)sin(bx)dx or z sin(ax)sin(bx)dx are usually done by using the addition formulas for the cosine and sine functions.

Web 1 Answer Sorted By:

If µ 2 r then eiµ def= cos µ + isinµ. To prove (10), we have: Web a cos(λt)+ b sin(λt) = a cos(λt − φ), where a + bi = aeiφ; Web we can use euler’s theorem to express sine and cosine in terms of the complex exponential function as s i n c o s 𝜃 = 1 2 𝑖 𝑒 − 𝑒 , 𝜃 = 1 2 𝑒 + 𝑒.